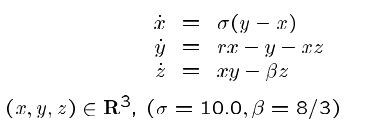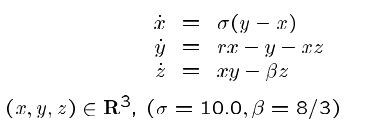Lorenz System*
This example helps illustrate that this approach turns numerical
instability into stability, by using a forward method in the stable
direction normal to the manifold, and a backward method in the unstable
direction normal to the manifold. The Lorenz system is a low order model of atmospheric circulation.
It is well-known for its chaotic attractor. At r=20.0, this system has
a saddle-type periodic orbit. For decreasing r, this periodic orbit
tends toward a homoclinic orbit. In this example, both the initial
closed curve and the initial hyperbolic splitting were determined by simulation,
hence were only roughly known. We continued the periodic orbit toward
the homoclinic orbit. Also illustrated below is the computed hyperbolic
splitting.
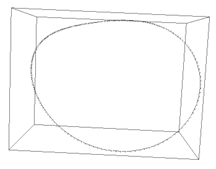 Periodic orbit of the Lorenz system, r=20.0,
discretized with 200 first order elements.
Periodic orbit of the Lorenz system, r=20.0,
discretized with 200 first order elements.
|
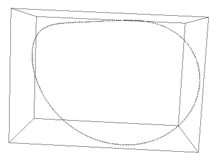 Periodic orbit of the Lorenz system, r=16.5,
200 first order elements.
Periodic orbit of the Lorenz system, r=16.5,
200 first order elements.
|

Hyperbolic Splitting of Periodic orbit of the Lorenz system, r=16.5,
discretized with 200 first order elements.
The user-written program which uses the class library to perform this
computation is provided as a class library usage example
.
3D-fattened Arnold map**

For small positive epsilon, this map has a saddle-type invariant closed
curve. The dynamics on the curve are quasiperiodic with phase locking
(thus the dynamics on the curve are determined by either a dense quasiperiodic
orbit or a finite number of fixed points). At about epsilon=0.49,
there is a saddle-node bifurcation, and a sink and a source appear on the
invariant curve. Normal hyperbolicity is lost at about epsilon=0.776.
In spite of the changing dynamics on the invariant curve, the continuation
illustrated below went very smoothly. Also visible in the pictures below is
the computed hyperbolic splitting.
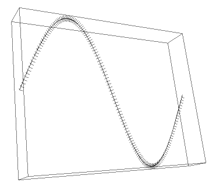
Closed curve of the fattened Arnold family, epsilon=0.0,
discretized with 50 third order elements.
|
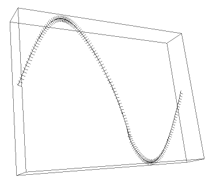
Closed curve of the fattened Arnold family,
epsilon=0.776,
discretized with 50 third order elements.
|
*C. Sparrow, ``The Lorenz equations: bifurcations, chaos, and strange
attractors,'' Springer-Verlag, New York, 1982.
**H. M. Osinga, ``Computing Invariant Manifolds,'' Ph.D. Thesis, University of
Groningen, The Netherlands, 1996.