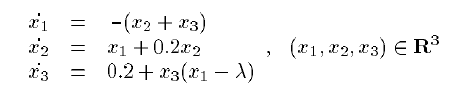
Rossler System*
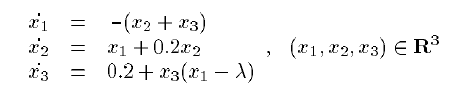
This system was proposed as a prototype system for modelling chaos. For lambda=2.2, the system has a stable periodic orbit, which undergoes a period-doubling bifurcation for increasing lambda. From initial data at lambda=2.2 (determined by simulation), we continued the periodic orbit for increasing lambda, as the orbit loses stability. Experiments indicate that while the orbit is attractive, the algorithm converges even when the initial data is quite far away (that is, there seems to be a large basin of attraction). Below is the last computed orbit, which is very near the bifurcation point.
The user-written program which uses the class library to perform this
computation is provided as a class library usage example
.
Van der Pol Equation**

Van der Pol's oscillator is a model of an RLC (electrical) circuit with a tunnel diode. This equation has a unique stable limit cycle for all positive epsilon, which becomes more and more singular for increasing epsilon. For epsilon=0.0, the circle with radius 2 is the limit cycle, and is taken as the initial data for the computation below.
*O. Rossler, Continuous chaos - four prototype equations, in O. Gurel & O. Rossler, eds, Bifurcation Theory and Applications in Scientific Disciplines, Ann. N.Y. Acad. Sci. 316 (1979), 376--392.
**B. Van der Pol, Forced oscillations in a circuit with nonlinear resistance, London, Edinburg and Dublin Philos. Mag. 3 (1927), 65--80.